Le forme della natura (alberi, foglie, coste, nuvole ecc.) mostrano quasi sempre un carattere irregolare e non possono essere rappresentati usando la geometria euclidea (cerchi, rette, poligoni).
Ad esempio in un albero (soprattutto nell'abete) ogni ramo è approssimativamente simile all'intero albero e ogni rametto è a sua volta simile al proprio ramo.
Per rimuovere questo ostacolo il matematico Benoit B. Mandelbrot (1982) ipotizzò un nuovo tipo di geometria: la geometria frattale.

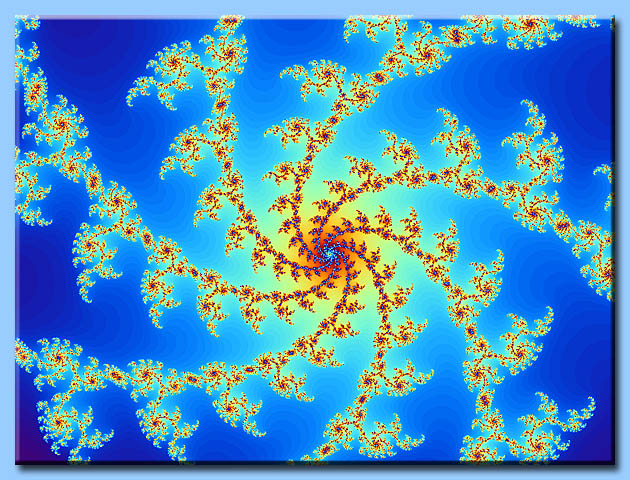
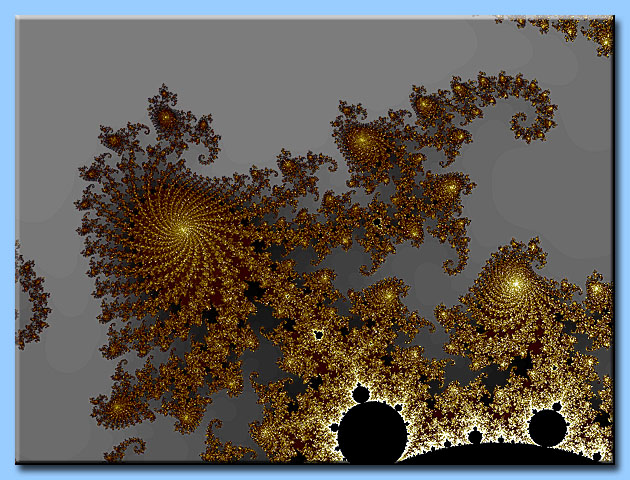
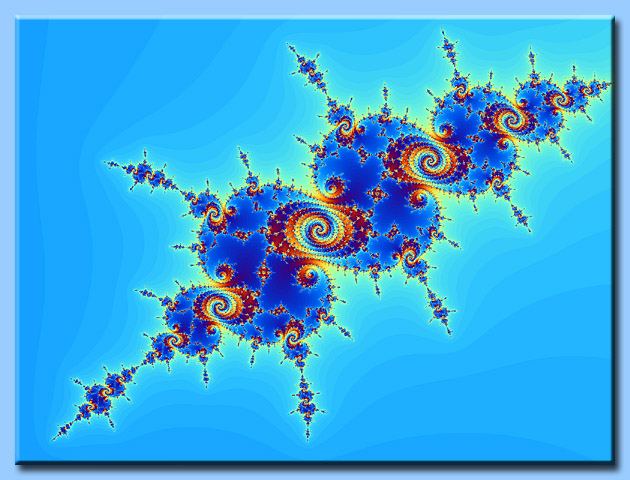
Una struttura frattale è una figura geometrica in cui un motivo si ripete su qualsiasi scala.
Ingrandendo la figura si noteranno forme ricorrenti e ad ogni ingrandimento essa rivelerà nuovi dettagli. Un frattale invece di perdere dettaglio quando è ingrandito, si arricchisce di nuovi particolari.

Il termine frattale, coniato da Mandelbrot, deriva dal termine latino 'fractus', che significa «irregolare e spezzato» L'insieme di Mandelbrot è un luogo geometrico del piano complesso e la sua frontiera (cioè il suo perimetro) è una curva frattale.

E' possibile riprodurre tale insieme utilizzando un computer e dei programmi che si possono trovare in rete. Nel mio caso, occupandomi di informatica, ho preferito scriverlo appositamente.

Gli algoritmi che generano i frattali, producono spesso delle immagini di grande bellezza, tanto che è nato un nuovo genere d'arte detta appunto arte frattale.